言語理論とコンパイラ
第三回:
有限オートマトンと線形文法
2012 年 4 月 27 日
http://www.sw.it.aoyama.ac.jp/2012/Compiler/lecture3.html
Martin J. Dürst

© 2005-12 Martin
J. Dürst 青山学院大学
今日の予定
- 前回の宿題
- 有限オートマトン
- 線形文法
- 正規表現
- それらの間の変換
前回の宿題
[都合により削除]
Cygwin のダウンロード、インストール
(提出なしだが、出来なかった人はノートパソコン持参)
自分のノートパソコンに cygwin をインストール (画像つき詳細)する。インストールの手順で必ず
gcc, flex, bisonと
make を選ぶ。
flex、bison、gcc
の動作確認
- Cygwin Bash Shell (または putty, mintty, Cygwin Terminal)
を起動
flex -V で flex のバージョン確認 (V
は大文字)bison -V で bison のバージョン確認 (V
は大文字)gcc -v で gcc のバージョン確認 (v
は小文字)make -v で make のバージョン確認 (v
は小文字)
前回のまとめ
| 文法 |
Type |
言語 |
オートマトン |
| 句構造文法 |
0 |
句構造言語 |
チューリング機械 |
| 文脈依存文法 |
1 |
文脈依存言語 |
線形拘束オートマトン |
| 文脈自由文法 |
2 |
文脈自由言語 |
プッシュダウンオートマトン |
| 正規文法 |
3 |
正規言語 |
有限オートマトン |
正規言語は字句解析に使用
今回の展望
- 有限オートマトン (finite state automaton, FSA)
- 決定性有限オートマトン (deterministic finite automaton,
DFA)
- 非決定性有限オートマトン (non-deterministic finite
automaton, NFA)
- 正規文法 (regular grammar)
- 左線形文法 (left linear grammar)
- 右線形文法 (right linear grammar)
- [正規表現 (regular expression)]
これらは全て同じ力を持って、正規言語を定義・受理する
有限オートマトン
- スタート状態から開始
- 入力の語を繰り返し一記号ごと読んで、これによって状態を遷移
- 語を読み終わった時点で受理状態にいるとこの語が受理
- 語を読み終わった時点で受理状態にいない、又は途中で動作不可の場合に語が非受理
- 状態の数が有限 (すなわち、メモリに制限)
(automaton (αὐτόματον) はギリシア語で、複数は
automata)
有限オートマトンの状態遷移図
(state transition diagram)
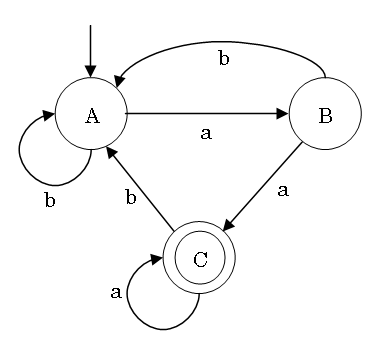
状態は丸、遷移はラベル付き矢印、外からの矢印は初期状態を示し、二重丸は受理状態
有限オートマトンの状態遷移表
(state transition table)
表の横は状態、縦は入力の記号、→は初期状態
(矢印がない場合、最初の状態が初期状態)、星は受理状態
有限オートマトンの定義
- 状態の有限集合 (Q、図の円、set of states)
- 入力記号の有限集合
(Σ、図の矢印のラベル、set of input symbols)
- 動作関数 (δ、図のラベル付き矢印
(状態遷移関数、state transition function))
- 初期状態 (q0 ∈
Q、図の外からの矢印のある円、表の矢印つき状態、start
state)
- 受理状態の有限集合 (F ⊆
Q、図の二重円、表の星つき状態、accepting
state/final state)
有限オートマトンは (Q, Σ, δ,
q0, F) の五字組で定義
決定性と非決定性有限オートマトン
|
決定性 (DFA) |
非決定性 (NFA) |
| 同時に |
一つの状態 |
複数の状態 (状態の集合) |
| 受理条件 |
現在の状態が受理状態 |
現在の状態の一つ以上が受理状態 |
| ε 遷移 |
不可 |
可能 |
| 動作関数の型 |
δ: Q × Σ → Q |
δ: Q × (Σ ∪ {ε})
→ P(Q) |
ε 遷移の扱い方
- 「普通」の遷移を行った後に、ε
遷移を実行
- ε 遷移は複数 (並行、立て続け) 実行可能
- ε 遷移は状態の移動ではなく、増加
- これを ε 閉包という (ε closure)
有限オートマトンの例
- ある一個の語だけ受理できる
- ある記号の数が奇数、偶数、3 で割れば余りが
2、等
- 語の先頭に決まった記号列がある
- 語の終わりに決まった記号列がある
- 語の真ん中に・どこかに決まった記号列がある
- 二つ以上の条件を同時に、または連続に、またはそのどちらかを満たすもの
NFA から同等の DFA への変換
- アルゴリズムの原理:
- NFA の状態の集合が DFA の状態
- NFA の初期状態の ε 閉包の集合が DFA
の初期状態
- NFA の受理状態を一つ以上含まれる DFA
の状態が受理状態
- 全ての NFA は同等の DFA に変換可能
- 全ての DFA は (単純な) NFA
- よって、DFA と NFA の受理能力が同等
- 実装は DFA の方が簡単が、テーブルの大きさが増加
NFA から同等の DFA への変換の一例
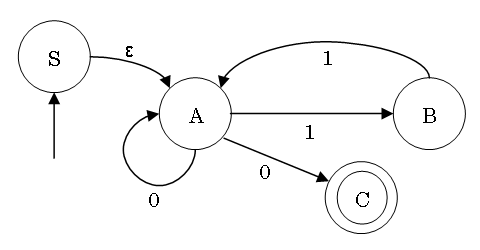
動作関数
|
ε |
0 |
1 |
| S |
{A} |
{} |
{} |
| A |
{} |
{A,C} |
{B} |
| B |
{} |
{} |
{A} |
| C |
{} |
{} |
{} |
DFA の最小化
ある DFA から同等の最小の DFA は次の通りに作れる:
- 状態を受理状態と非受理状態の二つの集合に分割
- それそれの状態からどの記号でどの集合に遷移するかを調査
- 現在の集合を、どの記号でも同じ集合に遷移する状態の部分集合に分割
- 3. で変更がない時まで 2. から繰り返す
最小化で:
- 効率よい実装が可能
- 二つの有限オートマトンが同等かどうかが簡単に判断可能
DFA の最小化の一例
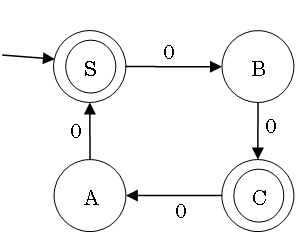
線形文法
(linear grammar)
文法の簡単な書換規則
| 規則の形 |
名称 |
| A → aB |
右線形規則 (非終端記号が右) |
| A → Ba |
左線形規則 (非終端記号が左) |
| A → a (又は A
→ε) |
定数規則 |
左線形文法 (left linear grammar):
左線形規則と定数規則しか含まない文法
右線形文法 (right linear grammar):
右線形規則と定数規則しか含まない文法
左線形文法と右線形文法はともに正規文法と言う
(一般の線形文法は文脈自由文法の一種)
(右) 線形文法と有限オートマトン
右線形文法と NFA の対応 (ε が考慮外):
- 状態は非終端記号と対応
- 初期状態は初期記号と対応
- 受理状態に遷移する動作は定数規則と対応
- 全ての動作は右線形規則と対応
左線形文法も同様 (語を右から読み込むと考えられる)
右線形文法と有限オートマトンの一例

A → aB | bA
B → bA | a | aC
C → bA | a | aC
今回まとめ
- 線形・正規文法、有限オートマトンは同等な言語を表現・受理
- DFA による効率の良い受理の実装が可能
- これらは字句解析に有効に使用可能
課題: NFA・DFA
は遷移表、遷移図、文法で表現可能が、もっとコンパクトな表現は?
宿題
提出期限と場所: 2012 年 5 月 10 日 (木) 19:00 まで O 棟 5
階の O-529 号室の前の箱に投入
形式: A4 一枚 (裏も使ってよい)
- 次の右線形文法に相当する NFA
の遷移図を作りなさい
S → εA | bB | cB | cC, A → bC | aD | a | cS, B → aD | aC | bB | a, C
→εA | aD | a
- 1. の NFA と同等の DFA を作りなさい
- 2. の DFA を最小化しなさい
flex, bison, gcc,
make の動作確認
(提出なしだが、出来なかった場合、必ず次回にノートパソコンを持参すること)




