Finite State Automata and Linear
Grammars
(有限オートマトンと線形文法)
Language Theory and Compilers
3rd lecture, April 27, 2018
http://www.sw.it.aoyama.ac.jp/2018/CP1/lecture3.html
Martin J. Dürst

© 2005-18 Martin
J. Dürst 青山学院大学
Today's Schedule
- Homework from last lecture
- Grammar types
- Finite state automata
- Linear grammars
- Conversions
Homework 1
For the language L = { a, cb, ac
}, list up the 10 shortest words of L*
Solution: 都合により削除
Additional problem (solution voluntary): List all words of
L* of length 4
Solution: 都合により削除
Homework 2
Problem: Using the grammar from the slide "Example of Grammar and
Derivation", find 3 words (different from each other and from
aabbaa). Give the full derivation for each word (rule numbers and
underlines not needed). Guess and explain what language this grammar defines
(Hint: If your guess is not simple, maybe you have made a mistake in the
derivations).
Grammar: 都合により削除
Solution example (partial):
都合により削除
Guess: The grammar defines the language with all the words of the form
anbnan (n≥1).
Homework 2 (Additional Problem)
Additional problem (solution voluntary): Prove your guess
Example solution summary:
都合により削除
Types of Grammars
Grammar types are distinguished by restrictions on rewriting rules:
0. No restrictions: Phrase structure grammar, (Chomsky) type 0
grammar
1. αAβ →
αγβ, where α and β
are sequences of 0 or more (non)terminals, and γ is a sequence of 1
or more (non)terminals:
Context-sensitive grammar, (Chomsky) type 1 grammar
2. A → γ, where γ is a sequence of 1 or
more (non)terminals:
Context-free grammar, (Chomsky) type 2 grammar
3. A → aB or A→ a
(alternative: A → Ba or A→
a):
Regular grammar, (Chomsky) type 3 grammar
(for all types, S → ε is also allowed)
Remarks on Homework 2
- The grammar can be changed to a context-sensitive grammar
by replacing the rule DC → CD with the four
rules
DC → QC, QC → QR,
QR → CR, and CR → CD.
- Languages such as anbnan can
be created with context-sensitive grammars, but not with context-free
grammars.
- This language is a context-sensitive language.
- This language is not a context-free language.
Cygwin Download and Installation
(no need to submit, but bring your note PC with you if you have problems)
On your notebook PC, install cygwin (detailled instructions
with screenshots).
Make sure you select/install all of gcc,
flex, bison, diff,
make and m4.
Checking flex, bison, gcc,...
Installation
To check your installation of the various programs, start up a Cygwin
Terminal session, and use the following commands to check the version of each
software:
flex -V (V is upper case)bison -V (V is upper case)gcc -v (v is lower case)diff -v (v is lower case)make -v (v is lower case)m4 --version
Summary of Last Lecture
| grammar |
type |
lanugage type |
automaton |
| phrase structure grammar (psg) |
0 |
phrase structure language |
Turing machine |
| context-sensitive grammar (csg) |
1 |
context-sensitive language |
linear-bounded automaton |
| context-free grammar (cfg) |
2 |
context-free language |
push-down automaton |
| regular grammar (rg) |
3 |
regular language |
finite state automaton |
Regular languages are used for lexical analysis.
Plan for this Lecture
- Finite state automata (FSA)
- Deterministic finite automaton (DFA)
- Non-deterministic finite automaton (NFA)
- Regular grammar
- Left linear grammar
- Right linear grammar
- [Regular expression]
These all are equivalent, and define/accept regular languages
Finite State Automaton Example
(automaton (αὐτόματον) is Greek; plural: automata)
Finite state automata are often represented with a state transition
diagram
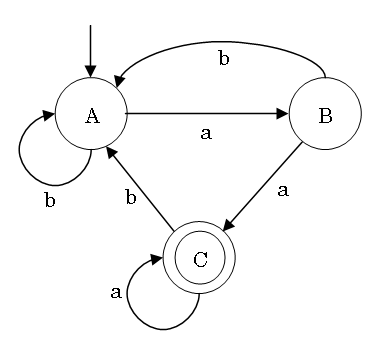
Arrow from outside: initial state
Circles: states
Double circles: accepting state(s)
Arrows with labels: transitions
Workings of a Finite State Automaton
- Start with initial state
- Repeatedly read one symbol of the input word,
and transition to the next state along the arrow with the corresponding
label
- If the automaton is in an accepting state at the end of the word,
then the word is accepted
- If the automaton is not in an accepting state at the end of the word,
or if there is no label with the right symbol, then the word is not
accepted
- The number of states is finite (i.e. there is only limited memory)
Examples of Finite State Automata
- Accepting only a word with a single specific symbol
- Accepting words where the number of symbols is odd, or even, or when
divided by 3, the reminder is 2,...
- Accepting words with a fixed sequence of symbols at the start
- Accepting words with a fixed sequence of symbols at the end
- Accepting words with a fixed sequence of symbols somewhere in the
middle
- Accepting words meeting more than one condition, at the same time or one
after the other, or one of more than one conditions
State Transition Tables
Finite state automata can also be represented with a state transition
table.
The state transition table for our example automaton is:
Leftmost column: state
Top row: input symbol
→: start state (first state if not otherwise indicated)
*: accepting state(s)
Table contents: state after transition
Formal Definition of FSAs
- A finite set of states Q (circles in diagram; leftmost column
in table)
- A finite set of input symbols Σ (arrow labels in diagram; top
row in table)
- A state transition function δ (arrows with labels in diagram;
contents of table)
- An initial state (start state) q0 ∈ Q
(circle with arrow from outside in diagram; state with arrow in table)
- A finite set of accepting (final) states F ⊆ Q
(double circles in diagram; states with asterisks in table)
A finite state automaton is defined as a quintuple (Q,
Σ, δ, q0, F)
Nondeterministic Finite Automata
- An FSA where there is always only one transition for each input is called
a deterministic finite automaton (or DFA)
- Other FSAs are called nondeterministic finite automata (or NFAs)
- If there are more than one possible transitions from a state on a given
input symbol, then:
- All transitions are executed simultaneously (as a result, the
automaton will be in multiple states)
- Further transitions also proceed alike (the number of occupied states
may increase further)
- Where there are no transitions, a state occupation will disappear
- At the end of the input, the word is accepted if at
least one of the occupied states is an accepting state
ε Transition
(epsilon transition)
- In NFAs, there are also ε transitions
- ε transitions are executed "for free", i.e. without any corresponding
input symbol
- ε transitions are executed immediately before starting, and immediately
after the "ordinary" transitions
- ε transitions may be executed in parallel or in
succession
- ε transitions increase the set of occupied states (rather than
moving)
- Executing all possible ε transitions is called ε
closure
Comparing DFAs and NFAs
|
Deterministic (DFA) |
Nondeterministic (NFA) |
| concurrently occupied states |
one single state |
multiple states (set of states) |
| acceptance criterion |
current state is accepting state |
one of the occupied states is accepting state |
| ε transition |
prohibited |
allowed |
| type of transition function |
δ: Q × Σ → Q |
δ: Q × (Σ ∪ {ε})
→ P(Q) |
(there are also NFAs without ε transition)
Equivalence of DFA and NFA
- NFAs look more complex and powerful than DFAs
- DFAs seem simpler to implement than NFAs
- Question: Are there languages that can be recognized by NFAs but not by
DFAs?
- Question: Is it possible to convert a(ny) NFA to an equivalent DFA?
Conversion from an NFA to an Equivalent DFA
- Algorithm principle:
- Each set of occupied states in the NFA becomes a state in the DFA
- The ε closure of the start state of the NFA becomes the
start state of the DFA
- Any set of states of the NFA that contains at least one accepting
state becomes an accepting state of the DFA
- All NFAs can be converted to equivalent DFAs
- All DFAs are (simple) NFAs
- Therefore, DFAs and NFAs have equivalent recognition power
- Implementing DFAs is very simple, but the size of the table needed may
grow
(worst case: n → 2n; most cases:
n → ~2n)
Example of Conversion from NFA to DFA
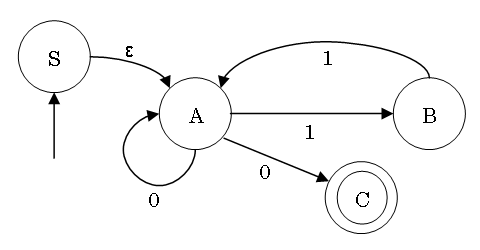
State Transition Table
|
ε |
0 |
1 |
| →S |
{A} |
{} |
{} |
| A |
{} |
{A,C} |
{B} |
| B |
{} |
{} |
{A} |
| *C |
{} |
{} |
{} |
Linear Grammar
Simple Rewriting Rules
| Rule Shape |
Name |
| A → cB |
right linear rule (nonterminal on the right) |
| A → Bc |
left linear rule (nonterminal on the left) |
| A → c |
constant rule |
A left linear grammar is a grammar only using left linear rules and
constant rules
A right linear grammar is a grammar only using right linear rules
and constant rules
(in both cases, a special rule S → ε is allowed)
Left linear grammars and right linear grammars are together called
linear grammars (or regular grammars)
(a grammar that contains both left linear rules and right linear rules is
not a linear grammar, but a kind of context-free grammar)
(Right) Linear Grammars and FSAs
Right linear grammars and NFAs correspond as follows (not considering
ε transitions):
- States correspond to nonterminal symbols
- The start state corresponds to the start symbol
- Transitions moving to an accepting state correspond to constant rules
- All transitions correspond to right linear rules
There is a similar correspondence for left linear grammars (imagine reading
the input backwards)
Example of Linear Grammar and NFA

A → aB | bA
B → bA | aC | a
C → bA | aC | a
Conversion between Right Linear Grammar and NFA
From automaton to grammar:
- Convert all states to nonterminal symbols (start state→start
symbol)
- Convert all transitions to right linear rules
- Convert all transitions to accepting states to constant rules
From grammar to automaton:
- Create a state for each nonterminal symbol (start symbol→start
state)
- Convert all right linear rules to transitions
- Create a new state only used for acceptance, and convert all constant
rules to transitions to this state
Today's Summary
- Linear/regular grammars and finite state automata generate/recognize the
same (class of) languages
- DFAs allow efficient inplementation of recognition of regular
languages
- This can be used for lexical analysis
Callenge: Regular languages can be represented by state transition
diagrams/tables of NFAs/DFAs, or with regular grammars, but a more compact
representation is desirable
Homework
Deadline: May 10, 2018 (Thursday), 19:00
Where to submit: Box in front of room O-529 (building O, 5th floor)
Format: A4 single page (using both sides is okay; NO cover page), easily
readable handwriting (NO printouts), name (kanji and kana) and student number
at the top right
- Draw a state transition diagram for a finite state automaton that
recognizes all inputs that (at the same time)
- Start with ab
- End with ba
- Contain an even number of c
- Draw the state transition diagram for the NFA in the state transition
table below
|
ε |
0 |
1 |
| →S |
{B} |
{C} |
{A} |
| A |
{C} |
{} |
{D, B} |
| B |
{} |
{D} |
{A} |
| *C |
{} |
{D} |
{A, B} |
| D |
{} |
{A, B} |
{} |
- Create the state transition table of the DFA that is equivalent to the
NFA in 2. (do not rename states)
- Check the versions of
flex, bison,
gcc, make, and m4 that you installed
(no need to submit, but bring your computer to the next lecture if you have
a problem)
Glossary
- Finite state automaton (FSA)
- 有限アウトマトン
- deterministic finite automaton (DFA)
- 決定性有限オートマトン
- Non-deterministic finite automaton (NFA)
- 非決定性有限オートマトン
- (left/right) linear grammar
- (左・右) 線形文法
- regular grammar
- 正規文法
- state transition diagram
- 状態遷移図
- transition
- 遷移
- initial/start state
- 初期状態
- accepting/final state
- 受理状態
- accept
- 受理する
- finite
- 有限
- state transition table
- 状態遷移表
- state transition function
- 動作関数
- simultaneous(ly)
- 同時 (な・に)
- ε transition
- ε 遷移
- ε closure
- ε 閉包
- equivalence
- 同等性
- (left/right) linear rule
- (左・右) 線形規則
- constant rule
- 定数規則
- renaming (of states)
- 状態の書換え



