From Lexical Analysis to
Parsing
(字句解析から構文解析へ)
6rd lecture, May 19, 2017
Language Theory and Compilers
http://www.sw.it.aoyama.ac.jp/2017/Compiler/lecture6.html
Martin J. Dürst

© 2005-17 Martin
J. Dürst 青山学院大学
Today's Schedule
- Minitest
- Remainders from last lecture
flex homework- Limitations of regular languages
- Differences between lexical analysis and parsing
- Context-free grammars
- Push-down automata
Minitest
flex Homework: Lexical Analysis for C
Deadline: May 25, 2017 (Thursday), 19:00, box in front of room O-529
(building O, 5th floor)
Additional Hints for Homework
- Start simple and proceed in small steps
- Command line for all steps:
flex xml.l && gcc lex.yy.c && ./a <flex_in.txt |
diff - flex_out.txt
- Example input,
output
Compilation Stages
- Lexical analysis
- Parsing (syntax analysis)
- Semantic analysis
- Optimization (or 5)
- Code generation (or 4)
Table of Formal Language Types
| grammar |
Type |
Lanugage type |
automaton |
| phrase structure grammar (psg) |
0 |
phrase structure language |
Turing machine |
| context-sensitive grammar (csg) |
1 |
context-sensitive language |
linear-bounded automaton |
| context-free grammar (cfg) |
2 |
context-free language |
push-down automaton |
| regular grammar (rg) |
3 |
regular language |
finite state automaton |
Limitations of Regular Languages/Grammars and FSAs
Can the following languages be represented with a regular expression?
- The language where all words consist of n
0es
followed by n 1s
- The language where all words consist of symbols
a,
b, and c so that words are palindromes (e.g.
acbca)
- The language where all words consist of the symbols
( and
), properly nested as in a formula
All these languages cannot be accepted by FSAs
because they have limited (finite) memory.
Comparing Lexical Analysis and Parsing
|
Lexical Analysis |
Parsing |
| Targets of analysis |
literals, identifiers, keywords, operators,... |
expressions, statements, functions, declarations, definitions,... |
| Requirement |
speed |
descriptive power |
| Notation |
regular expression |
context-free grammar |
| device for (automatic) analysis |
finite state automaton |
push-down automaton |
Regular Grammars and Context-Free Grammars
Regular grammar:
- Right linear grammar or left linear grammar
Context free grammar:
- The left hand side of all rewriting rules is a single non-terminal
symbol
- The right hand side is not restricted (any number of terminal and
non-terminals possible)
- Examples: A → cBd, B → ccB, S → cBcAd
- Meaning of free: Not dependent, not influenced by
- For programming languages, the correctness of syntax can be decided
locally, and does not depend on context
(however, there may be semantic constraints, e.g. whether a variable is
defined or not, and what type it has)
Example of Context-Free Grammar
S → aSa | bSb | c
Examples of generated words: c, aca, bcb,
abaabcbaaba
Language being generated: A single c in the middle,
surrounded by 0 or more a and b so that the resulting word is a
palindrome
This language cannot be accepted by an automaton with finite memory (e.g.
FSA)
We need to extend FSAs to create more powerful automata
We will add a push-down stack
Push-Down Stack and Push-Down Symbols
- A push-down stack stores push-down symbols
- Push-down symbols are different from input symbols
- Only the symbol on the top of the stack can be seen/checked
- Symbols can be added to or removed from the stack one at a
time
- There is a special symbol at the bottom of the stack, the bottom
marker
- The bottom marker cannot be removed
Example of Push-Down Automaton
- Σ = {a, b, c}
- The stack symbols are A, B, and Z (bottom marker)
- The stack is written with the top on the left
- A/ε means that if the top of the stack is A, then remove A
- A/A means that if the top of the stack is A, then leave it as is
- A/BA means that if the top of the stack is A, then replace that with BA
(i.e. put B on top)
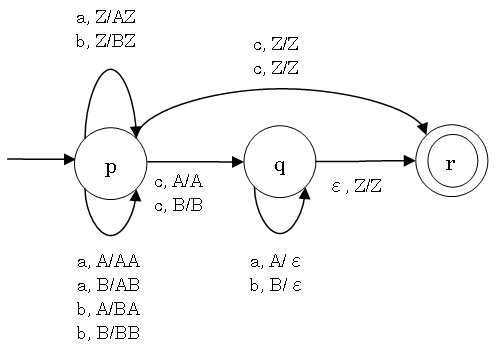
How a Push-Down Automaton Works
- In many ways the same as for FSAs (states, start state, final states,
transitions,...)
- At the start, the bottom marker is visible (i.e. the stack is empty)
- The transition is selected based on:
- The next input symbol (examples: a, b), and
- The stack symbol visible on the top of the stack (examples: B, Z)
- A transition is one of:
- Remove one symbol from the top of the stack (example: b, B/ε)
- Keep the stack as is (example: c, A/A)
- Put a new symbol on top of the stack (example: a, B/AB)
- The input is accepted if (variants can be shown to be equivalent):
- The bottom marker is visible
- The automaton is in a final state at the end of the input
- Both conditions (1. and 2.) are met
Deterministic and Nondeterministic Push-Down Automata
- The grammar S → aSa | bSb | c can be accepted by a deterministic
push-down automaton
- The grammar S → aSa | bSb | ε cannot be accepted by a deterministic
push-down automaton
Why: There is no marker in the middle of the
word
- Different from FSAs, the power of deterministic and nondeterministic
push-down automata is different
- For efficient parsing, it is important to use a grammar with a
deterministic pushdown automaton
- Fortunately, this is easy for programming languages
(there are other aspects of context-free languages/grammars that affect
parsing speed)
Homework
(bring to next lecture, will be collected)
For a programming language that you know (e.g. C, Java, Ruby,...), search
for a grammar on the Web, print it out, and carefully study it.
Glossary
- unsigned
- 符号無し
- nested
- 入れ子 (になっている)
- palindrome
- 回文、左右対称な語
- push-down symbol
- プッシュダウン記号
- bottom marker
- ボトムマーカ
- deterministic push-down automaton
- 決定性プッシュダウンオートマトン
- nonteterministic push-down automaton
- 非決定性プッシュダウンオートマトン

