Regular Expressions
(正規表現)
4rd lecture, April 28, 2017
Language Theory and Compilers
http://www.sw.it.aoyama.ac.jp/2017/Compiler/lecture4.html
Martin J. Dürst

© 2005-17 Martin
J. Dürst 青山学院大学
Today's Schedule
- Last week's homework, leftovers
- Minimization of DFAs
- Regular Expressions
- Formal definition
- Conversion to an NFA
- Conversion from an FSA
- Regular expressions in practice
Homework Due April 13
Last Week's Homework 1
Last Week's Homework 2
Last Week's Homework 3
Last Week's Homework 4
Check the versions of flex, bison,
gcc, make,m4 that you installed (no need
to submit, but bring your computer to the next lecture if you have a
problem)
Leftovers from Previous Lecture
Today's Outlook
Summary from last time:
- Finite state automata (FSA): deterministic finite automata (DFA) and
non-deterministic finite automata (NFA)
- Regular grammar: left linear grammar and right linear grammar
- All these have the same power, generating/recognizing regular
languages.
Callenge: Regular languages can be represented by state transition
diagrams/tables of NFAs/DFAs, or with regular grammars, but a more compact
representation is desirable.
There is a very powerful way to represent regular languages, called
regular expressions
Minimization of DFAs
To create the smallest DFA equivalent to a given DFA:
- Separate states into two sets, accepting states and non-accepting
states
- For each state, check which other states are reached for each input
symbol
- Partition each set of states into sets that can reach the same set with
the same input symobls
- Repeat 2. and 3. until there is no further change
Purpose of minimization:
- Efficient (minimum memory) implementation
- Deciding whether two FSAs are equivalent
(they are equivalent if their minimized DFAs are isomorphic)
Example of DFA Minimization
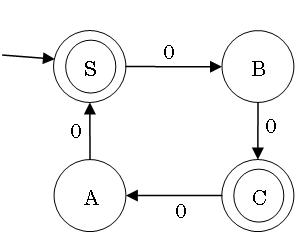
Efficient Implementation of a DFA
State next_state[state_count][symbol_count]; /* state transition table */
Boolean final_state[state_count]; /* final state? */
State current_state = start_state;
Symbol next_symbol;
while ((next_symbol=getchar()) != EOF && /* end of input */
current_state != no_state) /* dead end */
current_state = next_state[current_state][next_symbol];
if (final_state[current_state])
printf("Input accepted!");
else
printf("Input not accepted!");
Application of Regular Expressions
Problem 04C1 of Computer Practice I: Convert &,
", ', < and
> in the input to &, ",
', <, and >, respectively.
One way to write this in Ruby:
gsub /"/, '"'
gsub /'/, "'"
gsub /</, '<'
gsub />/, '>'
gsub /&/, '&'
gsub replaces all occurrences of a give pattern in a string
// are the delimiters for regular expressions (in Ruby, Perl,
JavaScript,...)
Examples of Regular Expressions
abc: {abc} (concatenation)a*: {ε, a, aa, aaa,...} (Kleene closure)a|b: {a, b} (alternative)ab|c*|d: {ab, ε, c, cc, ccc,..., d}a(b|c)*d: {ad, abd, acd, abbd, abcd, acbd, accd,...}
Purpose of Regular Expressions
- It is possible to use a regular grammar to define a regular language
- A grammar has multiple rewriting rules, and is difficult to
understand
- A single regular expression can represent a whole regular
language.
This regular expression is easy to write and read because it is short.
Notation of Regular Expressions
- Only characters themselves, concatenation, alternative, and repetition
are represented
- "Usual" characters represent themselves
- A small set of characters has a special role (meta-characters:
|, *, (, ), ε)
- Meta-characters may have to be escaped
Formal Definition of (Theoretical) Regular Expressions
Regular Expressions over Alphabet Σ
| Priority |
Regular Expression |
Condition |
Defined Language |
Notes |
|
ε, a |
a ∈ Σ |
{ε} or {a} |
literals
|
| very high |
(r) |
r is a regular expression |
L((r)) = L(r) |
grouping
|
| high |
r* |
r is a regular expression |
L(r*) = (L(r))* |
Kleene closure |
| low |
rs |
r, s are regular expressions |
L(rs) =
L(r)L(s) |
concatenation |
| very low |
r|s |
r, s are regular expressions |
L(r|s) = L(r) ∪
L(s) |
set union |
L(r) is the language defined by regular expression
r
Caution: Priority
Make sure you understand the difference between the following pairs of
regular expressions:
- abc* vs. (abc)*
- a|b|c* vs. (a|b|c)*
- ab|c vs. a(b|c)
Grammar for Regular Expressions
- Regular expressions also form a language
(set of all regular expressions)
- This is not a regular language, but a context-free language
- Grammar: R → ε, R →a, R →b,..., R
→R|R, R →RR,
R →R*, R →(R)
- The alphabet of a regular expression is the alphabet of the target
language (e.g. a, b,...) and the meta-characters (ε, |, *, (, ))
Examples of Regular Expressions
- One single word:
abc
- Number of symbols: even (
(aa)*), odd (a(aa)*),
reminder is 2 when divided by 3 (aa(aaa)*),...
- A specific symbol sequence at the start of a word:
abc(a|b|c)*
- A specific symbol sequence at the end of a word:
(a|b|c)*abc
- A specific symbol sequence in the middle of a word:
(a|b|c)*abc(a|b|c)*
From Regular Expression to NFA (Symbols, Alternatives)
An NFA for a regular expression is recursively constructed from the
subexpressions of the regular expression
For each subexpression, there is one start state and one accepting state.
These states are connected to form larger automata for larger regular
expressions.
The NFA for ε or a has a start state and an accepting
state, connected with a single arrow labeled as ε or
a
The NFA for r|s is constructed from the NFAs for
r and s as follows:
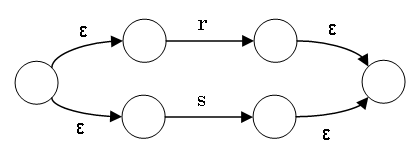
The additional ε connections are necessary to clearly commit to
either r or s.
From Regular Expression to NFA (Concatenation, Repetition)
The NFA for the regular expression rs connects the
accepting state of the NFA of r with the start state of the NFA of
s through an ε transition. The overall start state is the start
state of r; the overall accepting state is the accepting state of
s.
The NFA for r* is constructed as follows:
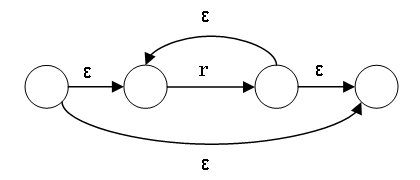
Example of Conversion
Regular expression: a|b*c
In some cases, some of the ε transitions may be eliminated, or the NFA may
otherwise be simplified.
From FSA to Regular Expression
Algorithmic conversion is possible, but complicated
General procedure:
- Create regular expressions for getting from state A to state
B directly for all pairs of states
- Select a single state, and create all regular expressions that pass
through this intermediate state
- Repeat step 2., increasing the number of intermediate states
- Simplify intermediate regular expressions as much as possible (they can
get quite complex)
When understanding what language the FSA accepts, it is often easy for
humans to create a regular expression for this language.
Applications of Regular Expressions
- Many different patterns can be expressed in a compact form
- Clear connection between theory and applications
- Built-in to many programming languages (Ruby,
Javascript, Perl, Python,...)
- Available as libraries in other programming languages (Java, C#,
C,...)
- Usable in many tools (e.g. plain text editors)
- Caution: Theoretical regular expressions and practical regular
expressions differ in many ways
Practical Regular Expressions:
Notational Differences
Practical regular expressions have many additional functions and shortcut
notations
(the corresponding theoretical regular expressions or simpler constructs are
given in parentheses)
.: a single arbitrary character (a|b|c|...)[acdfh]: character class: select a single character
((a|c|d|f|h))[b-f]: shortcut for continuous range in character class
((b|c|d|e|f))- r
+: one or more occurrences of r
(rr*)
- r
?: r or nothing (r|ε, ε
cannot be used in practical regular expressions
- r
{m,n}:
between m and n repetitions of r
(r...rr?...r?)
\*,...: \ escapes meta-characters- Meta-characters:
|*+?()[]{}.\^$
Practical Regular Expressions:
Usage Differences
- Theory: match a full word; practice: match part of a string
^/$ match the start/end of a string or line- The result of the match is not just yes/no, but includes the position of
the match, the substring matched, the substrings before/after the
match,...
- If there are multiple possible matches, the leftmost, longest match is
choosen
(leftmost is more important than longest)
- Parts of a string matching parts of a regular expression in parentheses
can be assigned to variables
- Partial matches can be reused inside the regular expression
Use of Practical Regular Expressions
- Text/document search
- String replacements (single or multiple)
- Cutting strings apart
Notes on Practical Regular Expressions
- Most regular expression engines are more powerful than DFA/NFA/regular
languages
- Most regular expression engines use backtracking
- Some regular expressions may be very slow on some input
Example: String an, regular expression
a?nan (n=3: string:
aaa, regular expression: a?a?a?aaa, really slow starting at , n~25)
- For further analysis, see e.g. https://regex101.com/
Summary of this Lecture
- Regular expressions, regular grammars, and finites state automata all
have the same power to generate/accept regular languages
- Regular expressions are a very compact representation
- DFAs are a very efficient way to implement recognition
- These are very useful for lexical analysis
- However, creating a DFA by hand from a regular expression is tedious
- However, because the number of states is finite, there are languages that
cannot be expressed, e.g. languages with corresponding pairs of
parentheses
Homework
Deadline: May 11, 2017 (Thursday), 19:00
Where to submit: Box in front of room O-529 (building O, 5th floor)
Format: A4 single page (using both sides is okay; NO cover page), easily
readable handwriting (NO printouts), name (kanji and kana) and student number
at the top right
- Construct the state transition diagram for the NFA corresponding to the
following grammar
S → εA | bB | cB | cC, A → bC | aD | a | cS, B → aD | aC | bB | a, C
→εA | aD | a
(Caution: In right linear grammars, ε is not allowed except in the rule S
→ ε)
(Hint: Create a new accepting state F)
- Convert the result of last week's homework 3 (after rewriting, see this
handout) to a right linear grammar
- Construct the state transition diagram for the regular expression
ab|c*d
(write down both the result of the procedure explained during this lecture
(with all ε transitions) as well as a version that is as simple as
possible)
- Bring your notebook PC (with
flex,
bison, gcc, make, diff,
and m4 installed and usable)
Glossary
- regular expression
- 正規表現
- minimization
- 最小化
- partition
- 分割
- delimiter
- 区切り文字
- alternative
- 選択肢
- repetition
- 繰返し
- meta-character
- メタ文字
- priority
- 優先度
- theoretical regular expressions
- 論理的 (な) 正規表現
- practical regular expressions
- 実用的 (な) 正規表現
- notation(al)
- 表記 (上の)
- arbitrary
- 任意
- leftmost
- できるだけ左



